Full covariance matrix of input data¶

This example demonstrates three ways to provide information about uncertainty of input data (here, of an imaginary time fermionic Green’s function \(G(\tau)\)),

As estimated error bars \(\sigma(\tau)\);
As a full covariance matrix \(\hat\Sigma_{\tau\tau'}\) ;
As a full covariance matrix \(\hat\Sigma_{\tau\tau'}\) with all eigenvalues shifted up by a constant \(l^2\), where \(l\) is so called filtering level.

Perform analytic continuation

# Import HDFArchive, some TRIQS modules and NumPy
from h5 import HDFArchive
from triqs.gf import *
import triqs.utility.mpi as mpi
import numpy as np

# Import main SOM class and utility functions
from som import Som, fill_refreq, reconstruct

n_w = 801                    # Number of energy slices for G(\omega)
energy_window = (-4.0, 4.0)  # Energy window to search solutions in

# Parameters for Som.accumulate()
acc_params = {'energy_window': energy_window}
acc_params['verbosity'] = 2  # Verbosity level
acc_params['l'] = 1000       # Number of particular solutions to accumulate
acc_params['f'] = 100        # Number of global updates
acc_params['t'] = 50         # Number of local updates per global update

# Read G(\tau) from an archive.
g_tau = HDFArchive('input.h5', 'r')['g_tau']
n_tau = len(g_tau.mesh)

# Estimated error bars on all slices of 'g_tau'
sigma = 0.01

#
# Construct a Som object using the estimated error bars.
#

error_bars = g_tau.copy()
error_bars.data[:] = sigma

cont_eb = Som(g_tau, error_bars, kind="FermionGf")

#
# Construct a Som object using a full covariance matrix.
#

# Create a GF container for the covariance matrix.
# It is defined on an 'n_tau x n_tau' mesh and has a 1D target shape
# with each target element corresponding to one diagonal element of 'g_tau'.
cov_matrix = Gf(mesh=MeshProduct(g_tau.mesh, g_tau.mesh),
                target_shape=(g_tau.target_shape[0],))

# Diagonal covariance matrix equivalent to using 'error_bars'
cov_matrix.data[:, :, 0] = (sigma ** 2) * np.eye(n_tau)
# Add slight correlations between adjacent \tau-slices
cov_matrix.data[:, :, 0] += np.diag(0.00005 * np.ones(n_tau-1), k=1)
cov_matrix.data[:, :, 0] += np.diag(0.00005 * np.ones(n_tau-1), k=-1)

cont_cm = Som(g_tau, cov_matrix, kind="FermionGf")

#
# Construct a Som object using the same covariance matrix and a finite filtering
# level.
#

# Before using the covariance matrix, SOM will shift its eigenvalues up by fl^2.
fl = 0.01
cont_cmfl = Som(g_tau, cov_matrix, kind="FermionGf", filtering_levels=[fl])

#
# Perform analytic continuation
#

for name, cont in (("error_bars", cont_eb),
                   ("cov_matrix", cont_cm),
                   ("cov_matrix_fl", cont_cmfl)):
    cont.accumulate(**acc_params)
    cont.compute_final_solution(verbosity=1)

    # Recover G(\omega) on an energy mesh
    g_w = GfReFreq(window=energy_window, n_points=n_w, indices=g_tau.indices)
    fill_refreq(g_w, cont)

    # G(\tau) reconstructed from the solution
    g_rec_tau = g_tau.copy()
    reconstruct(g_rec_tau, cont)

    # On master node, save results to an archive
    if mpi.is_master_node():
        with HDFArchive("results.h5", 'a') as ar:
            ar.create_group(name)
            gr = ar[name]
            gr['g_tau'] = g_tau
            gr['g_w'] = g_w
            gr['g_rec_tau'] = g_rec_tau

Download input file input.h5.

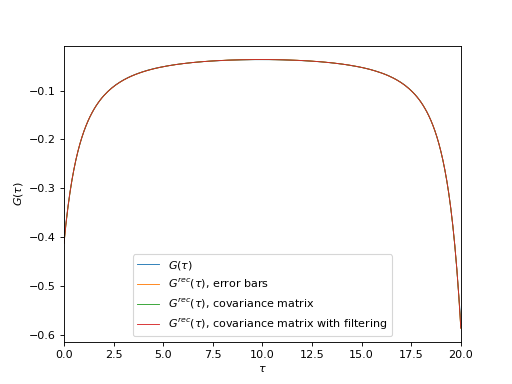
Plot input and reconstructed imaginary-time GF’s

from h5 import HDFArchive
from triqs.gf import *
from matplotlib import pyplot as plt
from triqs.plot.mpl_interface import oplot

# Read data from archive
ar = HDFArchive('results.h5', 'r')

g_tau = ar['error_bars']['g_tau']

# Plot input and reconstructed G(\tau)
oplot(g_tau, mode='R', lw=0.8, label=r"$G(\tau)$")
oplot(ar['error_bars']['g_rec_tau'][0, 0], mode='R', lw=0.8,
      label=r"$G^{rec}(\tau)$, error bars")
oplot(ar['cov_matrix']['g_rec_tau'][0, 0], mode='R', lw=0.8,
      label=r"$G^{rec}(\tau)$, covariance matrix")
oplot(ar['cov_matrix_fl']['g_rec_tau'][0, 0], mode='R', lw=0.8,
      label=r"$G^{rec}(\tau)$, covariance matrix with filtering")

plt.xlim((0, g_tau.mesh.beta))
plt.ylabel(r"$G(\tau)$")
plt.legend(loc="lower center")

(Source code, png, hires.png, pdf)

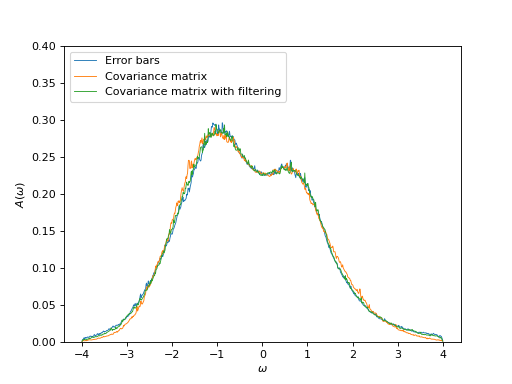
Plot spectral functions

from h5 import HDFArchive
from triqs.gf import *
from matplotlib import pyplot as plt
from triqs.plot.mpl_interface import oplot

# Read data from archive
ar = HDFArchive('results.h5', 'r')

# Plot spectral functions
oplot(ar['error_bars']['g_w'][0, 0],
      mode='S', lw=0.8, label=r"Error bars")
oplot(ar['cov_matrix']['g_w'][0, 0],
      mode='S', lw=0.8, label=r"Covariance matrix")
oplot(ar['cov_matrix_fl']['g_w'][0, 0],
      mode='S', lw=0.8, label=r"Covariance matrix with filtering")

plt.ylim((0, 0.4))
plt.ylabel(r"$A(\omega)$")
plt.legend(loc="upper left")

(Source code, png, hires.png, pdf)